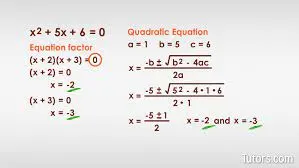The study of mathematics is essential for solving real-world problems and understanding the world around us. One of the most critical topics in mathematics is quadratic equations. Quadratic equations solve various issues in
- Physics
- Engineering
- Economics
- and other fields.
In this mathematical journey, Throughout this mathematical exploration, we’ll delve into the origin and uses of quadratic formulas.
What’s a Quadratic Equation?
A quadratic equation is a polynomial equation of the second degree, indicating that the variable’s highest power is 2. Its standard form is ax^2 + bx + c = 0.
Here, a, b, and c represent constants, while x stands for the variable. The values assigned to a, b, and c dictate the appearance of the graph for this quadratic equation, recognized as a parabola.
Derivation of Quadratic Formulas
The quadratic formula is to solve any quadratic equation in its general form. This formula’s derivation can be found by completing the square method or using the quadratic formula proof.
Completing the square is a method that entails adjusting the coefficients of a given quadratic equation until it transforms into a perfect square. This meticulous and time-intensive procedure eventually gives rise to the quadratic formula. This formula typically represents a quadratic equation
��2+��+�=0ax2+bx+c=0 derived through the process of completing the square. We can transform this equation into its equivalent form, (x – m)2 = n, where m and n are constants. Here, we have an equation for x, giving us the quadratic formula: x = (-b ±√(b2 – 4ac)) / 2a.
Applications of Quadratic Formulas
The quadratic formula has many practical applications in various fields. One such application is in physics, which calculates objects’ motion under constant acceleration. For example, in projectile motion problems, we use the quadratic formula to find the time it takes for an object to reach its maximum height and the distance traveled at a given time.
The quadratic formula works in economics to find optimal solutions for profit-maximizing equa0tions. It can also work in geometry to determine the coordinates of the vertex of a parabola or to find the roots of an equation representing a circle.
Determine the Nature of Roots
The discriminant is a term used in quadratic equations to determine the nature of its roots. It is calculated using the formula b2 – 4ac.
The coefficient
b represents the coefficient of x, while c signifies the constant term. The discriminant’s value serves as an indicator, revealing whether a quadratic equation possesses two real solutions, one real solution, or no real solutions.
The surge in popularity of online discriminant calculators has simplified the task for students and professionals in determining the discriminant of a provided quadratic equation. These calculators accept the input values of a,b, and c and swiftly generate the discriminant value, eliminating the need for manual calculations and streamlining the process for greater efficiency.
Types of roots based on discriminant values
As mentioned earlier, the discriminant of a quadratic equation can determine the nature of its roots. If the value of the discriminant is positive, then the equation has two distinct real solutions. When graphed, the parabola will intersect with the x-axis at two points.
The discriminant of a quadratic equation can take on three possible values: positive, negative, or zero. Each value corresponds to a different type of solution for the equation.
The equation will have two distinct real solutions if the discriminant is positive. This means the parabola will intersect with the x-axis at two points, giving us two answers.
Using Calculator
A calculator must first have a quadratic equation in its general form ax2 + bx + c = 0. Then, input the values of a, b, and c into the respective fields on the calculator. The result will be the value of the discriminant (b2 – 4ac).
If the discriminant is positive, the equation has two distinct real roots. If the discriminant is zero, there is only one real root for the equation. And if the discriminant is negative, there are no real solutions to the quadratic equation.
A Discriminant Calculator is helpful for students learning about quadratic equations and their applications. It allows them to check if they have correctly solved a quadratic equation by calculating the discriminant and determining the number of natural solutions.
Conclusion
In conclusion, delving into quadratic equations stands as a crucial part of mathematical study, offering numerous real-world applications. The quadratic formula emerges as an efficient means to solve these equations, while calculators simplify root determination.
With these resources at their disposal, both students and professionals can delve deeper into understanding quadratic equations and their significance in solving real-world issues. Grasping the concepts, derivation, and practical uses of quadratic equations remains essential.
Let’s persist in our mathematical journey, uncovering the myriad wonders and applications of the quadratic formula.